Résumé
La deuxième heure a été consacrée à la relation entre deux modèles fondamentaux, le modèle vibratoire en temps continu et le modèle synchrone en temps discret. J’ai pris comme illustration les circuits combinatoires, moteurs de tous les ordinateurs actuels. Les mêmes notions se retrouveront dans les cours suivants sur des exemples logiciels.
Vibration et synchronisme dans les circuits combinatoires
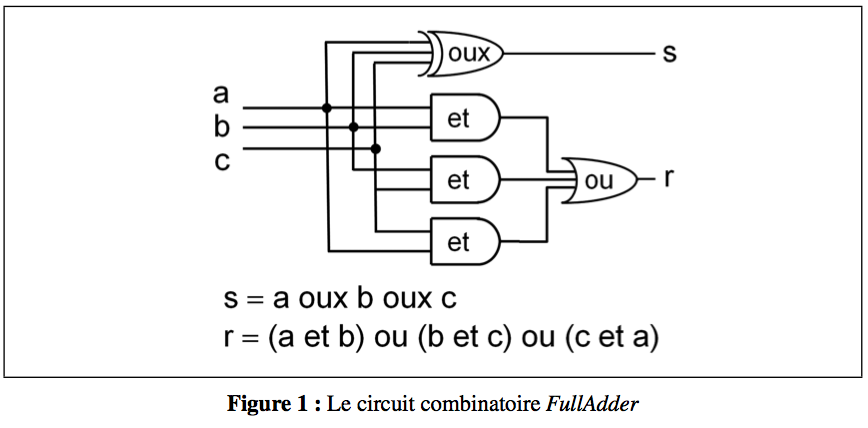
Considérons le circuit combinatoire FullAdder défini indifféremment par le dessin ou les équations de la figure 1, « oux » dénotant la fonction « ou exclusif ». Il possède trois bits d’entrées a, b et c, et calcule deux bits en sortie, leur somme s et leur retenue r. Il doit être vu de deux façons. Dans la vision vibratoire, iciélectronique, il est constitué de fils et de portes construites avec des transistors. Si on applique des voltages binaires aux entrées, par exemple 0 V ou 1 V, les fronts électriques se propagent dans les fils à la vitesse de la lumière et les portes calculent dynamiquement le voltage de leur sortie en fonction de celui de leurs entrées. Ceci se réalise en temps fini et prévisible (minorable) par les électroniciens. Voici pourquoi. La propagation électrique se fait en parallèle dans le réseau. Chaque fil introduit un délai dépendant de son implantation sur la puce. Chaque porte introduit un délai dépendant du montage de ses transistors, de la température, et de ses valeurs d’entrées. Mais ces délais sont bornés et le circuit est acyclique : on peut donc calculer le plus long délai d’une entrée quelconque à une sortie quelconque, appelé délai critique ; les chemins correspondants sont appelés chemins critiques. Au plus tard après le délai critique, les voltages sont partout stables et les sorties valent les valeurs booléennes déterminées par les opérations logiques des portes en fonction des entrées. Le circuit se comporte comme une machine vibratoire déterministe, avec une propriété fondamentale de confluence : quel que soit l’ordre de propagation des fronts, qui dépend de l’implantation et de la température, le résultat final est le même [1].