Abstract
Sequential circuits
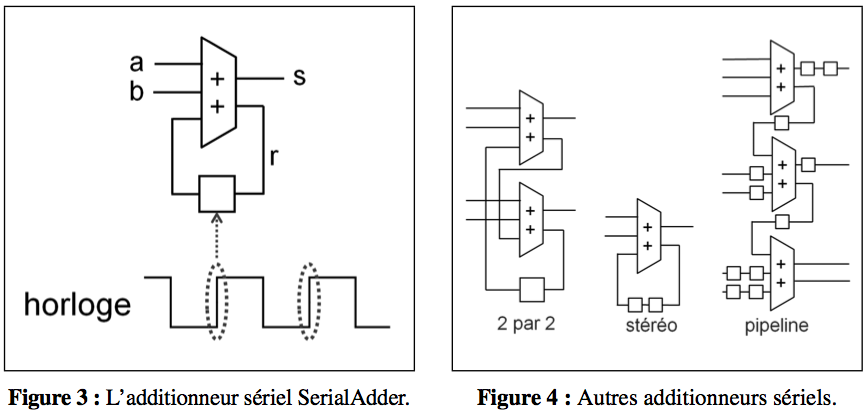
In synchronous circuits, operations follow one another in discrete time steps. A synchronous circuit is made up of two conceptually distinct but physically intertwined parts: the Combinatorics part, on which the computation is based at each instant, and the registers, which store the values from one instant to the next. The registers are governed by a clock, which produces square-wave signals of which only the rising edges are of interest here. At each rising edge, the registers simultaneously sample and store the values of their inputs [1], then propagate these values to their outputs for the entire next cycle. A register is therefore a shifter with respect to discrete time. For simplicity's sake, we'll assume that the registers are initialized to 0 at the first cycle. For the calculation to run smoothly, it must be guaranteed that the time distance between successive rising edges of the clock is greater than the sum of the critical delay of the Combinatorics part and the register changeover time (usually much less): a synchronous circuit can therefore only operate at 1 gigahertz if this sum is less than 1 nanosecond. In the figures, a register will be drawn as a square.
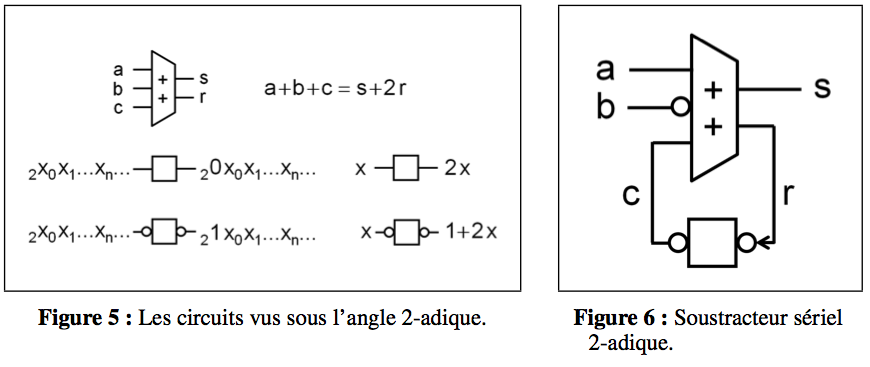 The remarkable work of Jean Vuillemin [2] establishes the relationship between 2-adics and circuits. The key points are summarized in Figure 5. Firstly, the FullAdder circuit finds in 2-adics a far more interesting definition than its purely Combinatorics definition in Fig. 1. If we denote a, b, c, s,r, the sequences of adder inputs and outputs over time seen as 2-adics, then FullAdder verifies the 2-adic invariant a + b + c = s + 2r, which advantageously replaces Boolean computation by numerical computation. The second point is that a register is a multiplier by 2 for 2-adics, since it outputs an initial 0 and then the delayed input bits. If we add a Boolean negation on each side of the register, represented by a circle, the resulting "ear register" calculates 1+2x for input x.
The remarkable work of Jean Vuillemin [2] establishes the relationship between 2-adics and circuits. The key points are summarized in Figure 5. Firstly, the FullAdder circuit finds in 2-adics a far more interesting definition than its purely Combinatorics definition in Fig. 1. If we denote a, b, c, s,r, the sequences of adder inputs and outputs over time seen as 2-adics, then FullAdder verifies the 2-adic invariant a + b + c = s + 2r, which advantageously replaces Boolean computation by numerical computation. The second point is that a register is a multiplier by 2 for 2-adics, since it outputs an initial 0 and then the delayed input bits. If we add a Boolean negation on each side of the register, represented by a circle, the resulting "ear register" calculates 1+2x for input x.